$\parbox{10cm}{\scriptsize\bf Universit\'e Paris-Descartes.\\ UFR de... ...} \ %{\large \bf Sujet 1 }\\ 45, rue des Saints-P\\lq eres 75270 Paris cedex 06}$

Mathématiques et Calculs : Correction du partiel n$^o1$
Octobre 2007

L1 : Licence sciences et technologies,
mention mathématiques, informatique et applications

Nombre de pages de l'énoncé : 2. Durée 1 h30.

NB : Ce sujet contient six questions à choix multiples et un exercice. Pour chaque question du questionnaire à choix multiples, cinq réponses sont proposées : deux réponses sont exactes et trois réponses sont fausses.

Question 1 Soit $(u_n)_{n\in \mathbb{N}}$ une suite réelle. Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

Si $(u_n)_{n\in \mathbb{N}}$ est positive et majorée, alors elle est convergente.

2. Oui     Non    

Si les sous-suites $(u_{2n})$ et $(u_{2n+1})$ convergent alors $(u_n)$ est convergente.

3. Oui     Non    

Si $(u_n)_{n\in \mathbb{N}}$ est minorée et décroissante, alors elle est convergente.

4. Oui     Non    

Si $(u_n)_{n\in \mathbb{N}}$ est convergente, alors toute sous-suite de $(u_n)_{n\in \mathbb{N}}$ est convergente.

5. Oui     Non    

$(u_n^2 \rightarrow l )\Rightarrow (u_n \rightarrow \sqrt{l})$.

Question 2 Soit $E$, $F$, $G$ trois parties quelconques d'un ensemble non vide $S$. $E^c$ désigne le complémentaire de $E$ dans $S$. Soit $P$ et $Q$ des propositions. Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

$[P \textit{ et } (P \Longrightarrow Q) ] \Longrightarrow Q$.

2. Oui     Non    

$E \cap (F^c \cup G)^c = E \cap F \cap G^c$.

3. Oui     Non    

$( E \cap F = E \cap G ) \Longrightarrow F = G$.

4. Oui     Non    

$E \cap (F \cup G) = (E \cup F) \cap (E \cup G)$.

5. Oui     Non    

$(P\Rightarrow Q) \Leftrightarrow ( (non P) \Rightarrow (non Q))$.

Question 3 Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

Les équations : $(3x+5) (2x+1) = 4x^2 -1$ et $3x+5=2x-1$ ont les mêmes solutions sur $\mathbb{R}$

2. Oui     Non    

L'ensemble des solutions de l'inéquation

$$\frac{x+1}{2x-3} \geq 0$$

est $]-\infty , \frac{3}{2}[ \cup ] \frac{3}{2}, 4[$

3. Oui     Non    

Pour tout $x, y \in \mathbb{R}$, si $0 \leq x \leq 2$ et $-3\leq y \leq -2$, alors $-4 \leq xy \leq 0$.

4. Oui     Non    

Pour tout $x\in \mathbb{R}$, $\vert x-1\vert<3 \Leftrightarrow -2<x <4$

5. Oui     Non    

Pour tout réels $a,b,x$ , $0 <a \leq x \leq b \Rightarrow \frac{1}{b} \leq \frac{1}{x} \leq \frac{1}{a}$

Question 4 Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

$e^{\frac{2i\pi}{3}} = -\frac{1}{2} - i\frac{\sqrt{3}}{2}$

2. Oui     Non    

$\forall \alpha \in \mathbb{R}$, $(e^{i\alpha })^{-1} = -e^{i\alpha}$

3. Oui     Non    

Tout polynôme de degré supérieur ou égal à un admet au moins une racine dans $\mathbb{C}$.

4. Oui     Non    

Soit $(z_n)$ une suite complexe. Si les suites $(Re(z_n))$ et $Im (z_n))$ convergent alors $(z_n)$ converge.

5. Oui     Non    

Les solutions dans $\mathbb{C}$ de l'équation $z^n=1$ sont de la forme : $z=e^{\frac{ik\pi }{n}}$, pour $k \in \{ 0, \dots , n-1 \}$.

Question 5 Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

La suite $(u_n)_{n\in \mathbb{N}}$ est bornée s'écrit : $\forall n \in \mathbb{N}, \exists M \in \mathbb{R}, : \vert u_n\vert \leq M$.

2. Oui     Non    

Soit $A\subset \mathbb{R}$, et $M\in \mathbb{R}$, alors : $M\geq Sup(A) \Rightarrow (\forall x \in A , x\leq M )$.

3. Oui     Non    

La suite $(u_n)_{n\in \mathbb{N}}$ tend vers $- \infty$ s'écrit : $\exists m < 0, \forall n \in \mathbb{N} : u_n < m$.

4. Oui     Non    

$\left[ \forall x \in E : x \in F \Longrightarrow x \in G \right]$ est équivalente à $(F \cap E) \subset G$.

5. Oui     Non    

L'ensemble $A$ est borné s'écrit: $\exists m \in \mathbb{R}, \; \forall x \in A, \; \exists M \in \mathbb{R}, \; m\leq x\leq M$.

Question 6 Parmi les propositions suivantes, déterminer les deux qui sont vraies.

1. Oui     Non    

$$\sum_{k=0}^n (k+1)^2=\left( \sum_{k=0}^n (k+1)\right)^2$$ ,      $\forall n \in \mathbb{N}$.

2. Oui     Non    

$\sum_{k=0}^{20} 1 = 20$.

3. Oui     Non    

$\sum_{k=1}^{n} \frac{(-1)^{2.k+1}}{2^k} = \frac{1}{2^n} - 1$.

4. Oui     Non    

$lim _{n\rightarrow +\infty } (\sum _{k=0}^n (-\frac{1}{3})^k ) =0$.

5. Oui     Non    

$\sum_{k=0}^{n} (-2)^k \binom{n}{k} = (-1)^n$.

Exercice Soit $(u_n)_{n\in \mathbb{N}}$ la suite réelle définie par

$$\begin{array}{l} u_0=4 \\ u_{n+1} = \sqrt{5u_n}, \forall n\in \mathbb{N} \end{array}$$

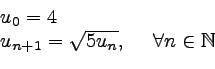
On constate que pour tout $n$, $u_n$ est strictement positif (Il n'est pas demandé de démontrer ce résultat.)

1)

$u_1 = 2 \sqrt{5}$, $u_2 = \sqrt{2} \sqrt{\sqrt{5}} \sqrt{5}$, $u_3 =\sqrt{5 \sqrt{5} \sqrt{2 \sqrt{5}}}$.

2)

On veut montrer que pour tout $n \in \mathbb{N}$, $u_n \leq 5$, en utilisant un raisonnement par récurrence.

a) pour $n=0$ : $u_0 =4 \leq 5$

b) Soit $n \in \mathbb{N}$ .

$$u_n \leq 5 \Rightarrow 5 u_n \leq 25$$

$$u_n \leq 5 \Rightarrow \sqrt{5 u_n} \leq 5$$

$$u_n \leq 5 \Rightarrow u_{n+1} \leq 5$$

Alors, d'après l'hypothèse de récurrence : $\forall n \in \mathbb{N}$, $u_n \leq 5$

3)

Nous avons : $\frac{u_{n+1}}{u_n} = \sqrt{\frac{5}{u_n}}$. Mais, comme $u_n \leq 5$, alors $\frac{u_{n+1}}{u_n} \geqslant1$. On conclut que $(u_n)_{n\in \mathbb{N}}$ est croissante car ses termes sont positifs.

4)

$(u_n)_{n\in \mathbb{N}}$ est croissante et majorée ; elle est donc convergente. En plus, sa limite $l$ vérifie $l=\sqrt{5l}$. Cette dernière équation possède deux solutions : 0 et $5$. Comme $u_n \geqslant4$, alors $l=5$.