| Université René Descartes |
| UFR Mathématiques et Informatique |
| 2004-2005 |
| Licence 1ère année, UE MC1 |
|---|
(a) Pour chaque question du questionnaire à choix multiples, quatre réponses
sont proposées : deux réponses sont exactes et deux réponses sont fausses. L'étudiant
répondra en cochant, sur la feuille de réponse jointe à l'énoncé, les deux cases des
réponses qu'il pense correctes. Les points ne seront accordés que si les deux réponses
correctes, et elles seules, ont été cochées. Aucun point ne sera accordé si une seule
réponse, même
correcte, est cochée. La feuille de réponse ne doit pas être raturée.
Tout document est interdit. Les calculatrices et les téléphones portables,
même à titre d'horloge, sont également interdits.
![]() On se place dans
On se place dans
![]() .
.
![]() On considère dans
On considère dans
![]() les
deux familles de vecteurs suivantes :
les
deux familles de vecteurs suivantes :
![]() et
et
![]() .
.
![]() On considère, dans
On considère, dans
![]() , la famille de vecteurs
, la famille de vecteurs
![]() .
.
![]() On considère les matrices :
On considère les matrices :
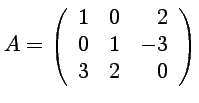 ,
,
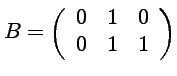 et
et
![]()
![]() On considère l'endomorphisme
On considère l'endomorphisme ![]() de
de
![]() défini par
défini par
![]() et la
matrice
et la
matrice
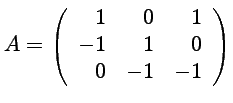 .
.
![]() Soit
Soit ![]() définie par
définie par
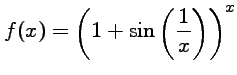
![]() Soit
Soit ![]() définie par
définie par
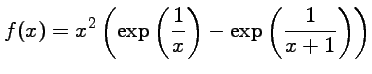
![]() Soit
Soit ![]() définie par
définie par
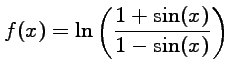
Remarque préliminaire : Les questions qui suivent nécessitent une
réponse rédigée. Les points ne seront attribués que si les
différentes étapes de la démonstration sont correctement et clairement
justifiées.
On se place dans
![]() et on considère l'endomorphisme
et on considère l'endomorphisme ![]() défini par
défini par
On pose
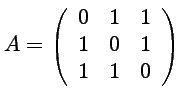 et
et
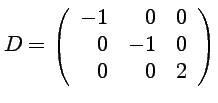 .
.
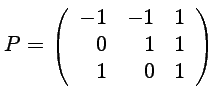
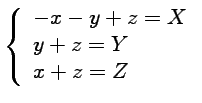
et expliquer comment en déduire que
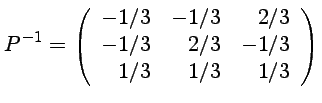 .
.
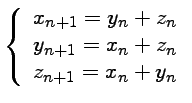
et on pose
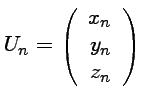 et
et
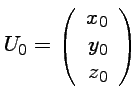 .
Trouver une relation matricielle enlatre
.
Trouver une relation matricielle enlatre
Nom :
Prénom :
n![]() carte d'étudiant :
carte d'étudiant :
| a | b | c | d | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 |