Restoration of images corrupted with Poisson noise

Observation model
Maximum A Posteriori: from Bayesian to variational framework
Primal-dual reformulation
Computational procedure
Example
- Basic tools for image manipulation in Scilab
- Simulations
Restoration using the Huber total variation
References

Observation model

Let $u: \Omega \to \RR_+$ be an (unobserved) intensity image defined on a discrete domain $\Omega$ (a rectangular subset of $\ZZ^2$). A photon count observation of the ideal image $u$ is the a random image $u_0 \in \NN^\Omega$ following the Poisson probability density function (p.d.f)

\begin{equation} \label{eq:likelihood} % p(u_0\,|\,u) = \prod_{(x,y) \in \Omega} \frac{u(x,y)^{u_0(x,y)}}{u_0(x,y)!} \, e^{-u(x,y)} \propto \exp{\left( - \langle u-u_0 \log{u} , 1_\Omega \rangle\right)} \;, % \end{equation}

where $1_\Omega$ denotes the constant image equal to $1$ on $\Omega$ and $u_0 \log{u}$ denotes a pointwise multiplication of the pixels of $u_0$ with those of $\log{u}$. The notation $\propto$ indicates an equality up to a global multiplicative constant (which depends on $u_0$ but not on $u$).

When $u_0(x,y) = 0$, whatever the value of $u(x,y)$ we have $u(x,y)^{u_0(x,y)} = 1$ therefore we have to take the convention that $u_0(x,y) \log{u(x,y)} = 0$ as soon as $u_0(x,y) = 0$ in \eqref{eq:likelihood}.

According to our model, if $u_0(x,y) > 0$ then necessarily $u(x,y) > 0$ (since when $u(x,y) = 0$ we observe $u_0(x,y) = 0$ with probability 1). Consequently, we need to add the convention that $u_0(x,y) \log{u(x,y)} = - \infty$ if $u_0(x,y) > 0$ and $u(x,y)=0$.

Maximum A Posteriori: from Bayesian to variational framework

Using the improper (discrete) $\TV$ prior $p(u) \propto e^{-\lambda \TV(u)}$ (where $\beta$ is a positive regularization parameter) and Equation \eqref{eq:likelihood}, we get thanks to the Bayes rule the posterior density

\begin{equation} \label{eq:posterior} % p(u \,|\, u_0) \propto p(u_0 \,|\, u) \, p(u) = \exp{ \left( - \langle u - u_0 \log{u} , 1_\Omega \rangle - \lambda \TV(u) \right) } \;. % \end{equation}

The Maximum A Posteriori (MAP) consists in computing the image that maximizes the posterior density $p(u \,|\,u_0)$, or equivalently that minimizes the convex energy $-\log{p(u \, | \, u_0)}$. Finally the MAP approach boils down to the variational problem

\begin{equation} \label{eq:primal-problem} % \widehat{u}_\text{MAP} = \arg\, \min_{u \in \RR_+^\Omega} \langle u - u_0 \log{u} , 1_\Omega \rangle + \lambda \TV(u) \;. % \end{equation}

From an optimization point of view, we see that the parameter $\lambda$ (that must be set by the user) controls the tradeoff between minimizing the total variation term $\TV(u)$ (called regularity term) and minimizing the opposite log-likelihood term $\langle u - u_0 \log{u} , 1_\Omega \rangle$ (called the data fidelity term).

Primal-dual reformulation

Recall the dual formulation of the discrete total variation (see here the page dedicated to the discrete total variation)

$$ \TV(u) = \max_{p \in \RRRR{\Omega}} \langle \nabla u , p \rangle \quad \text{subject to} \quad \|p\|_{\infty,2} \leq 1 \;, $$

where $\|p\|_{\infty,2} = \max_{(x,y) \in \RR^\Omega} \|p(x,y)\|_2$.

Noting $\delta$ the indicator function of the closed unit ball of the norm $\|\cdot\|_{\infty,2}$, that is

\begin{equation} \forall p \in \RRRR{\Omega}, \quad \delta(p) = \left\{ \begin{array}{cl} 0 & \text{if } \|p\|_{\infty,2} \leq 1 \\ +\infty & \text{otherwise,} \end{array} \right. \end{equation}

and replacing the $\TV$ term by its dual formulation into equation \eqref{eq:primal-problem} we obtain a primal-dual (saddle-point) reformulation of problem \eqref{eq:primal-problem},

\begin{equation} \label{eq:primal-dual-problem} % \hat{u}_\text{MAP} = \arg \, \min_{u \in \RR_+^\Omega} \, \max_{p \in \RRRR{\Omega}} \langle u - u_0 \log{u} , 1_\Omega \rangle + \langle \lambda \nabla u , p \rangle - \delta(p) \;, % \end{equation}

that can be numerically solved thanks the Chambolle and Pock algorithm [3].

Computational procedure

The Chambolle and Pock algorithm

A solution of problem \eqref{eq:primal-dual-problem} can be numerically computed using the algorithm of Chambolle-Pock [3], which is designed to solve the generic saddle-point problem

\begin{equation} \label{eq:cp.primal-dual} \arg\,\min_{x \in X}\max_{y \in Y} ~ G(x) + \langle Kx , y \rangle - F^\star(y) \;. \end{equation}

The algorithm is briefly presented on this page.

Taking $X=\RR_+^\Omega$, $Y=\RRRR{\Omega}$, $(x,y) = (u,p)$, $F^\star(p) = \delta(p)$, $G(u) = \langle u - u_0 \log{u} , 1_\Omega \rangle$ and $K = \lambda \nabla$ into problem \eqref{eq:cp.primal-dual} allows to recover problem \eqref{eq:primal-dual-problem}.

Noting $\divergence = -\nabla^*$ the opposite of the adjoint of the operator $\nabla$ (in analogy with the continuous setting), we have $K^* = -\lambda \divergence$, then the Chambolle and Pock algorithm applied to problem \eqref{eq:primal-dual-problem} boils down to Algorithm 1.

Chambolle-Pock resolvant algorithm for problem \eqref{eq:primal-dual-problem}.

Initialization: Choose $\tau, \sigma > 0$, $\theta \in [0,1]$, $u^0 \in \RR^\Omega$, $p^0 \in \RRRR{\Omega}$ and set $\bar{u}^0 = u^0$.

Iterations ($k \geq 0$): Update $u^k,p^k$ and $\bar{u}^k$ as follows

\begin{eqnarray} p^{k+1} &=& \arg\,\min\limits_{\substack{p \in \RRRR{\Omega} }} ~ \tfrac{1}{2\sigma} \left\|p-(p^k+\sigma \lambda \nabla \bar{u}^k)\right\|_2^2 + \delta(p) \label{cp.dual} \\ u^{k+1} &=& \arg\,\min\limits_{\substack{u \in \RR_+^\Omega}} ~ \tfrac{1}{2\tau} \left\|u-\left(u^k +\tau \lambda \divergence p^{k+1} \right)\right\|_2^2 + \langle u - u_0 \log{u} , 1_\Omega \rangle \label{cp.primal} \\ \bar{u}^{k+1} &=& u^{k+1} + \theta \left(u^{k+1}-u^{k}\right) \nonumber \end{eqnarray}

$~$

Notice that the convergence of Algorithm 1 toward the (here unique) solution of problem \eqref{eq:primal-dual-problem} is ensured when $\theta = 1$ and $\tau \sigma {|||K|||}^2 < 1$. Here we have ${|||K|||}^2 = \lambda^2 {|||\nabla|||}^2$, wich depends on the choice of the discretization scheme used for $\nabla$.

The primal and dual updates (Equations \eqref{cp.primal} and \eqref{cp.dual}) can be computed in closed-form.

The dual update \eqref{cp.dual} boils down to the pointwise operations $$ % \forall (x,y) \in \Omega, \quad p^{k+1}(x,y) = \frac{p^k(x,y) + \sigma \lambda \nabla \bar{u}^k(x,y) }{\max { \left( 1 , \left|\, p^k(x,y) + \sigma \lambda \nabla \bar{u}^k(x,y) \,\right|_2 \right) }} \;, % $$ and the primal update \eqref{cp.primal} boils down to the pointwise operations $$ \forall (x,y) \in \Omega, \quad u^{k+1}(x,y) = \frac{\left(s_0(x,y)-\tau\right) + \sqrt{\left(s_0(x,y) - \tau \right)^2 + 4 \tau u_0(x,y)} }{2}\;. $$ where we have set $s_0(x,y) = u^k(x,y) + \tau \lambda \divergence{p^{k+1}}(x,y)$.

Computing the solution of the dual update problem \eqref{cp.dual} is straightforward, we will focus on the primal update problem \eqref{cp.primal} that must be carrefully handled although it does not raise any great difficulty.

Solving \eqref{cp.primal} amounts to solve for any $(x,y) \in \Omega$ the subproblem

\begin{equation} \label{eq:primal-update-xy} % u^{k+1}(x,y) = \arg \, \min_{s \geq 0} \tfrac{1}{2\tau} \left(s - s_0(x,y)\right)^2 + s - u_0(x,y) \log{s} \;. % \end{equation}

First when $u_0(x,y) = 0$, we have set $u_0(x,y)\log{s} = 0$ for any $s$ (recall Remark 1), we easily show that the solution of \eqref{eq:primal-update-xy} is $u^{k+1}(x,y) = \max{ \left( 0 , s_0(x,y) - \tau \right)}$, that can be written
$$u^{k+1}(x,y) = \frac{(s_0(x,y)-\tau) + \left| s_0(x,y)-\tau\right| }{2} = \frac{\left( s_0(x,y) - \tau \right) + \sqrt{ \left( s_0(x,y) - \tau \right)^2 + 4 \tau u_0(x,y)} }{2} \;, $$

since $u_0(x,y) = 0$.
Now when $u_0(x,y) > 0$, thanks to Remark 2 we know that $0$ is not a solution of \eqref{eq:primal-update-xy} since $-u_0(x,y) \log{s} = +\infty$ when $s=0$. Therefore, problem \eqref{eq:primal-update-xy} boils down to
$$u^{k+1}(x,y) = \arg \, \min_{s > 0} f(s) := \tfrac{1}{2\tau} \left(s - s_0(x,y)\right)^2 + s - u_0(x,y) \log{s} \;,$$

which is a convex and differentiable problem. To solve the problem we need to find a critical point of $f$ into $\RR_{++}$. Finding a critical point of $f$ amounts to solve a quadratic equation, we get

$$ f'(\hat{s}) = 0 \Leftrightarrow \hat{s} \in \{\hat{s}_+,\hat{s}_-\} \quad \text{where} \quad \hat{s}_{+/-} = \frac{\left( s_0(x,y) - \tau \right) \pm \sqrt{ \left( s_0(x,y) - \tau \right)^2 + 4 \tau u_0(x,y)} }{2} \;.$$

and since $u_0(x,y) > 0$, we have $\hat{s}_- < 0$ and $\hat{s}_+ >0$. Finally we conclude that $u^{k+1}(x,y) = \hat{s}_+$.

Discretization schemes

Let $n_x$ and $n_y$ denote the width and height of the initial (noisy) image $u_0$, we note $\Omega = \left\{ 1, \dots , n_x \right\} \times \left\{ 1, \dots , n_y \right\}$ the discrete domain of $u_0$. We propose here to use the following finite difference scheme for the gradient operator

$$ \forall u \in \RR^\Omega, \quad \forall (i,j) \in \Omega, \quad \nabla u (i,j) = \left( \nabla_x u (i,j), \nabla_y u (i,j) \right)\;, $$

where

\begin{equation*} % \nabla_x u (i,j) = \left\{ \begin{array}{cl} u(i+1,j) - u(i,j) & \text{if } i < n_x \\ 0 & \text{if } i=n_x \end{array} \right. % \quad % \nabla_y u (i,j) = \left\{ \begin{array}{cl} u(i,j+1) - u(i,j) & \text{if } j < n_y \\ 0 & \text{if } j = n_y \end{array} \right. % \end{equation*}

This operator is easily implementable in Scilab langage,

function [Dx,Dy] = grad(u)
  [ny,nx] = size(u);
  Dx = u(:,[2:nx,nx]) - u;
  Dy = u([2:ny,ny],:) - u;
endfunction

and we can prove that the corresponding divergence operator (the opposite of the adjoint of $\nabla$) is given by

$$ \forall p = (p_x,p_y) \in \RRRR{\Omega}, \quad \forall (i,j) \in \Omega, \quad \divergence{(p)}(i,j) = \text{div}_x (p_x)(i,j) + \text{div}_y (p_y)(i,j) \;, $$

where

\begin{equation*} % \text{div}_x (p_x)(i,j) = \left\{ \begin{array}{cl} p_x(i,j)-p_x(i-1,j) & \text{if } 1 < i < n_x \\ p_x(i,j) & \text{if } i = 1 \\ -p_x(i-1,j) & \text{if } i = n_x \\ \end{array} \right. % \quad % \text{div}_y (p_y)(i,j) = \left\{ \begin{array}{cl} p_y(i,j)-p_y(i,j-1) & \text{if } 1 < j < n_y \\ p_y(i,j) & \text{if } j = 1 \\ -p_y(i,j-1) & \text{if } j = n_y \\ \end{array} \right. \end{equation*}

This operator is also easily implementable in Scilab langage.

function d = div(px,py) // compute d = div(p) where p = (px,py) and size(px) == size(py)
  [ny,nx] = size(px);
  div_x      =  px - px(:,[1,1:(nx-1)]);
  div_x(:,1) =  px(:,1);
  div_x(:,nx) = -px(:,nx-1);
  div_y      =  py - py([1,1:(ny-1)],:);
  div_y(1,:) =  py(1,:);
  div_y(ny,:) = -py(ny-1,:);
  d = div_x + div_y;
endfunction

Scilab implementation of the Chambolle Pock algorithm

With the choice of discretization scheme described in the previous section, we can show that the induced $\ell^2$ norm of the operator $\nabla$ is less than $\sqrt{8}$ (that is ${|||\nabla|||} \leq \sqrt{8}$), then if $K = \lambda \nabla$, we have ${|||K|||} \leq L := \lambda \sqrt{8}$, therefore taking $\tau = \sigma = \tfrac{0.99}{L}$ into Algorithm 1 ensures that $\tau \sigma \, {|||K|||}^2 < 1$ (which, in addition to the setting $\theta=1$ is sufficient to ensure the convergence of the algorithm toward the solution of problem \eqref{eq:primal-dual-problem}).

We have now all the information necessary to implement Algorithm 1.

//        TV restoration of Images Corrupted with Poisson noise
//
// u0 = input image
// lambda = regularity parameter (TV weight)
// niter = number of iterations for the Chambolle-Pock algorithm
// u = restored image
// E = energy (E(i) = energy computed at iteration i)
//
function [u,E] = tvdenoise_poisson(u0,lambda,niter)
  //* initialization *//
  [ny,nx] = size(u0);
  E = zeros(niter,1);
  Omega0 = (u0 > 0);
  u = u0;
  ubar = u0;
  px = zeros(u0);
  py = zeros(u0);
  // precompute Chambolle & Pock algorithm step parameters
  tau = 0.99/(sqrt(8)*lambda);
  sigma = tau;
  theta = 1;
  //*************** main loop ***************//
  for i = 1:niter
    //* compute (Dx,Dy) = grad(ubar) *//
    [Dx,Dy] = grad(ubar);
    //* update p = (px,py) *//
    px  = px + sigma*lambda*Dx;
    py  = py + sigma*lambda*Dy;
    nrm = px.*px + py.*py;
    id = nrm > 1; nrm = sqrt(nrm(id));
    px(id) = px(id) ./ nrm;
    py(id) = py(id) ./ nrm;
    // * compute d = div(p) *//
    d = div(px,py);
    //* update u and ubar *//
    ubar = -theta * u;
    s0 = u + tau*lambda*d;
    u = 0.5 * ((s0-tau) + sqrt((s0-tau).^2+4*tau*u0));
    ubar = ubar + (1+theta)*u;
    //* compute energy of u *//
    [Dx,Dy] = grad(u);
    tv = sum(sqrt(Dx.^2 + Dy.^2));
    E(i) = sum(u)-sum(u0(Omega0).*log(u(Omega0))) + lambda*tv;
    printf("iteration %d : E = %.10g\n",i,E(i));
  end
  //************ end of main loop ************//
endfunction

Example

Basic tools for image manipulation in Scilab

We first propose some very basic tools dedicated to image manipulation in Scilab (opening, visualization, Poisson noise).

Image viewer

function imview(u)
  [height,width] = size(u);
  fg = figure();
  set(fg,"axes_size",[width,height],"infobar_visible","on","menubar_visible","on","toolbar_visible","off","auto_resize","off","color_map",graycolormap(256));
  set(fg.children,"margins",zeros(1,4));
  Matplot(255/(%eps+max(u)-min(u)) * (u-min(u)),"010",[1,1,width,height]);
endfunction

Image opening (format PMG)

// open a PGM RAW image (8 bits)
// usage: u = readpgm('lena.pgm');
function image=readpgm(filename)
  //* local function *//
  function l=getline(u)
    h=[]
    while %t
      c=mget(1,'uc',u)
      if c==10 then break, end
      h=[h c]
    end
    l=ascii(h)
  endfunction
  //* main *//
  [u,err]=mopen(filename,'rb')
  if err<>0 then error('Impossible to open file '+filename), end
  if getline(u)~='P5' error('Unrecognized format'), end
  z=getline(u), while part(z,1)=='#', z=getline(u), end
  execstr('n=['+z+']')
  getline(u)
  image=matrix(mget(n(1)*n(2),'uc',u),n)'
  mclose(u)
endfunction

Generate photon count observation (Poisson noise)

// compute a Poissonian observation of u
function v = poisson_noise(u)
  v = zeros(u);
  for i=1:length(u)
    v(i) = grand(1,1,'poi',u(i));
  end
endfunction

Simulations

The reference image actin.pgm used in this section is downloadable in PGM RAW format here (licence: CC public domain, source (first channel)).

Create the noisy image and restore it using Algorithm 1

//* Open the reference image *//
ref = readpgm('actin.pgm'); // change the path according to the location of the image on your disk
imview(ref); // display reference

//* Generate noisy observation *//
u0 = poisson_noise(ref); // generate u0 = Photon count observation of ref.
imview(u0); // display u0

//* Run tvdenoise algorithm *//
lambda = 0.07; // set regularity parameter
niter = 200;  // choose a number of iterations for the Chambolle-Pock algorithm
[u,E] = tvdenoise_poisson(u0,lambda,niter);
imview(u); // display output (restored)
figure(); plot(1:niter,E); // plot energy evolution
xlabel("iteration"); ylabel("energy");
title("Energy decrease");

reference	photon-count observation $u_0$
$~$
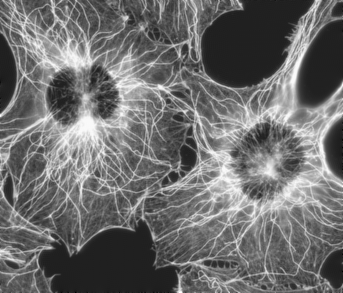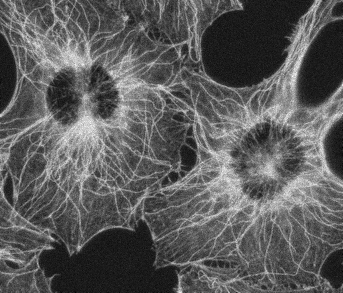energy decrease	restored ($\lambda=0.07$)
$~$

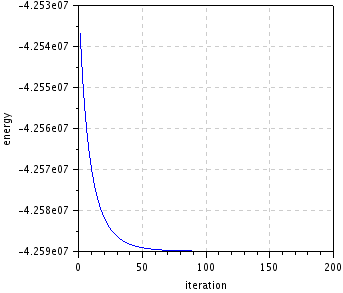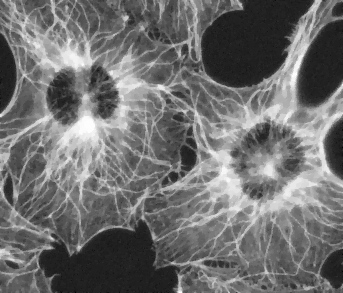display details (crop and nearest-neighbor zoom)

imview(ref(90:199,135:244).*.ones(3,3)); // display details of the reference image
imview(u0(90:199,135:244).*.ones(3,3)); // display details of the noisy image u0
imview(u(90:199,135:244).*.ones(3,3)); // display details of the restored image u

details of $u_0$	details of the restored image	details of the reference image
$~$	$~$

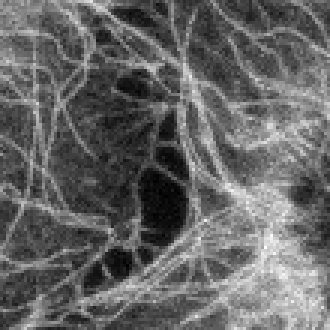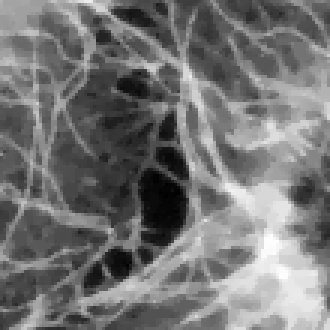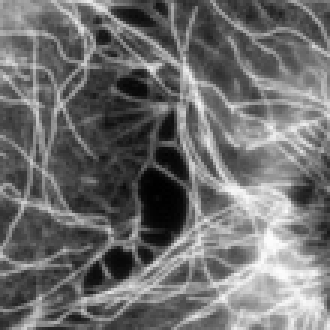Restoration using the Huber total variation

The use of the discrete total variation as a regularizer for image processing applications has a main drawback, the so-called staircasing effect that is the creation of piecewise constant regions with artificial boundaries in the restored image. This undesirable effect has been rigorously identified and studied in [5,6,7], in particular it is proven (in a more general setting than total variation regularization) in [5] that the non-differentiability at zero of the total variation is responsible of the staircasing artifact.

In order to get rid of the staircasing artifact, we can to replace the $\ell^2$ norm $|\cdot|_2$ of the gradient by the Huber-function $|\cdot|_\alpha$, defined as

\begin{equation*} % \forall g \in \RR^2, \quad |g|_\alpha = \left\{ \begin{array}{cl} \frac{|g|_2^2}{2\alpha} & \text{if } |g|_2 \leq \alpha\;, \\ | g |_2 - \frac{\alpha}{2} & \text{otherwise}\;, \end{array} \right. % \end{equation*}

which is a smooth approximation of the $\ell^2$-norm (near $0$ the $\ell^2$ norm is being replaced by a quadratic $\ell^2$ norm).

Given a parameter $\alpha > 0$, the (discrete) Huber total variation with smoothness parameter $\alpha$ writes

$$\forall u \in \RR^\Omega, \quad \HTValpha (u) = \sum_{(x,y) \in \Omega} \left| \nabla u (x,y) \right|_\alpha \;, $$

The primal problem

The Huber total variation variant of the initial problem consists in replacing the $\TV$ regularizer by $\HTValpha$, the problem writes

\begin{equation} \label{eq:primal-problem-huber} % \widehat{u}_\text{MAP}^\text{Huber} = \arg\, \min_{u \in \RR_+^\Omega} \langle u - u_0 \log{u} , 1_\Omega \rangle + \lambda \HTValpha(u) \;. % \end{equation}

Primal-dual formulation

The dual formulation (see the proofs here) of $\HTValpha$ is given by

\begin{equation*} % \forall u \in \RR^\Omega, \quad \HTValpha(u) = \max_{p \in \RRRR{\Omega}} \langle \nabla u , p \rangle - \tfrac{\alpha}{2} \|p\|_2^2 \quad \text{subject to} \quad \|p\|_{\infty,2} \leq 1 \;, % \end{equation*}

replacing accordingly the $\HTValpha$ term in \eqref{eq:primal-problem}, we get a primal-dual reformulation of the problem

\begin{equation} \label{eq:primal-dual-huber} % \widehat{u}_\text{MAP}^\text{Huber} = \arg\, \min_{u \in \RR_+^\Omega} \, \max_{p \in \RRRR{\Omega}} \langle u - u_0 \log{u} , 1_\Omega \rangle + \langle \lambda \nabla u , p \rangle - \delta(p) - \lambda \tfrac{\alpha}{2} \|p\|_2^2\;, % \end{equation}

Chambolle-Pock algorithm. Replacing function $\delta(p)$ by $\delta(p)+\lambda \tfrac{\alpha}{2} \| p \|_2^2$ into Algorithm 1, leads to a resolvant algorithm for problem \eqref{eq:primal-dual-huber}. Note that only the dual update is changed and we easily derive a closed-form formula.

Replacing $\delta(p)$ by $\delta(p)+\lambda \tfrac{\alpha}{2} \|p\|_2^2$ into Equation \eqref{cp.dual} (the dual update of Algorithm 1), boils down to the pointwise operations $$ % \forall (x,y) \in \Omega, \quad p^{k+1}(x,y) = \frac{\left(p^k(x,y) + \sigma \lambda \nabla \bar{u}^k(x,y) \right) / \nu }{\max { \left( 1 , \left|\, \left( p^k(x,y) + \sigma \lambda \nabla \bar{u}^k(x,y) \right) / \nu \,\right|_2 \right) }} \;, % $$ where $\nu = 1+\sigma \alpha \lambda$.

Scilab implementation

//        Huber-TV restoration of Images Corrupted with Poisson noise
//
// u0 = input image
// alpha = Huber smoothness parameter
// lambda = regularity parameter (TV weight)
// niter = number of iterations for the Chambolle-Pock algorithm
// u = restored image
// E = energy (E(i) = energy computed at iteration i)
//
function [u,E] = htvdenoise_poisson(u0,alpha,lambda,niter)
  //* initialization *//
  [ny,nx] = size(u0);
  E = zeros(niter,1);
  Omega0 = (u0 > 0);
  u = u0;
  ubar = u0;
  px = zeros(u0);
  py = zeros(u0);
  // precompute Chambolle & Pock algorithm step parameters
  tau = 0.99/(sqrt(8)*lambda);
  sigma = tau;
  theta = 1;
  nu = 1+sigma*alpha*lambda;
  //*************** main loop ***************//
  for i = 1:niter
    //* compute (Dx,Dy) = grad(ubar) *//
    [Dx,Dy] = grad(ubar);
    //* update p = (px,py) *//
    px  = (px + sigma*lambda*Dx)/nu;
    py  = (py + sigma*lambda*Dy)/nu;
    nrm = px.*px + py.*py;
    id = nrm > 1; nrm = sqrt(nrm(id));
    px(id) = px(id) ./ nrm;
    py(id) = py(id) ./ nrm;
    // * compute d = div(p) *//
    d = div(px,py);
    //* update u and ubar *//
    ubar = -theta * u;
    s0 = u + tau*lambda*d;
    u = 0.5 * ((s0-tau) + sqrt((s0-tau).^2+4*tau*u0));
    ubar = ubar + (1+theta)*u;
    //* compute energy of u *//
    [Dx,Dy] = grad(u);
    nrm = Dx.^2 + Dy.^2;
    id = (nrm <= alpha^2);
    htv = 0.5/alpha*sum(nrm(id)) + sum(sqrt(nrm(~id))-alpha/2);
    E(i) = sum(u)-sum(u0(Omega0).*log(u(Omega0))) + lambda*htv;
    printf("iteration %d : E = %.10g\n",i,E(i));
  end
  //************ end of main loop ************//
endfunction

Example

//* Open the reference image *//
ref = readpgm('actin.pgm'); // change the path according to the location of the image on your disk
imview(ref); // display reference

//* Generate noisy observation *//
u0 = poisson_noise(ref); // generate u0 = Photon count observation of ref.
imview(u0); // display u0

//* Run tvdenoise algorithm *//
lambda = 0.07; // set regularity parameter
niter = 200;  // choose a number of iterations for the Chambolle-Pock algorithm
alpha = 10;   // set the Huber smoothness parameter
u_iso = tvdenoise_poisson(u0,lambda,niter);
u_hub = htvdenoise_poisson(u0,alpha,lambda,niter);

//* display details (crop and nearest neighbor zoom) *//
imview(ref(90:199,135:244).*.ones(3,3));   // display reference image (crop & zoom)
imview(u0(90:199,135:244).*.ones(3,3));    // display noisy image (crop & zoom)
imview(u_iso(90:199,135:244).*.ones(3,3)); // display TV restored image (crop & zoom)
imview(u_hub(90:199,135:244).*.ones(3,3)); // display HTV restored image (crop & zoom)

reference	noisy observation

isotropic $\TV$ ($\lambda=0.07$)	Huber $\TV$ ($\lambda=0.07$, $\alpha=10$)
$~$

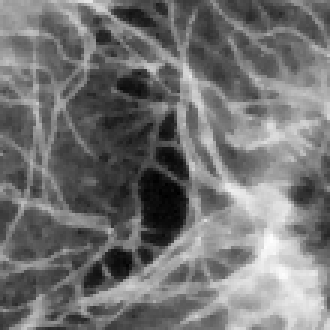The Huber variant of the initial model does not introduce any numerical nor mathematical difficulty and leads to more natural images free of staircasing artifact, although a bit less sharp than those obtained with the initial model.

References

Rudin, L. I., Osher, S., and Fatemi, E.: ``Nonlinear total variation based noise removal algorithms'', Physica D 60(1), pp. 259–268, 1992.
Ekeland, I., and Témam, R.: ``Convex analysis and variational problems'', volume 28 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, english edition, 1999. Translated from the French.
Chambolle, A., Pock, T.: ``A first-order primal-dual algorithm for convex problems with applications to imaging'', Journal of Mathematical Imaging and Vision, vol. 40, pp. 120–145, 2011.
Chambolle, A., Caselles, V., Cremers, D., Novaga, M., and Pock, T.: `` An introduction to total variation for image analysis'', Theoretical foundations and numerical methods for sparse recovery, 9, 263–340, 2010.
Nikolova, M.: ``Local Strong Homogeneity of a Regularized Estimator'', SIAM Journal on Applied Mathematics, vol. 61, pp. 633–658, 2000.
Chan, T. F., Marquina, A., and Mulet, P.: ``Higher Order Total Variation-Based Image Restoration'', SIAM Journal on Scientific Computing, vol. 22, pp. 503–516, 2000.
Ring, W.: ``Structural Properties of Solutions to Total Variation Regularization Problems'', M2AN, Modélisation Mathématique et Analyse Numérique, vol. 34, pp. 799–810, 2000.
Louchet, C., and Moisan, L.: ``Total variation denoising using iterated conditional expectation'', In proceedings of the European Signal Processing Conference (Eusipco), 2014.

reference	photon-count observation \(u_0\)
\(~\)
energy decrease	restored (\(\lambda=0.07\))
\(~\)

details of \(u_0\)	details of the restored image	details of the reference image
\(~\)	\(~\)

reference	noisy observation

isotropic \(\TV\) (\(\lambda=0.07\))	Huber \(\TV\) (\(\lambda=0.07\), \(\alpha=10\))
\(~\)